
- Auteur Lynn Donovan [email protected].
- Public 2023-12-15 23:46.
- Dernière modifié 2025-01-22 17:24.
Nous sommes maintenant prêts à discuter de deux dimensions tableaux , appelé matrices (singulier: matrice ). UNE matrice ressemble à un tableau avec des lignes et des colonnes. Il est possible pour tableaux avoir plusieurs dimensions. Un tridimensionnel déployer , par exemple, a 3 indices, où chaque dimension est représentée en indice dans le déployer.
De cette manière, qu'est-ce qu'un tableau matriciel ?
Déployer : Collection d'éléments homogènes. Matrice : Une simple ligne et colonne. Les deux sont des choses différentes dans des espaces différents. Mais en programmation informatique, une collection de dimensions uniques déployer peut être qualifié de matrice . Vous pouvez représenter un Tableau 2D (c'est-à-dire, collection de dimension unique tableaux ) dans matrice former.
De même, un tableau 2D est-il une matrice ? Comme un 1D déployer , une Réseau 2D est un ensemble de cellules de données, toutes du même type, auxquelles on peut attribuer un nom unique. Cependant, un Réseau 2D est organisé comme un matrice avec un certain nombre de lignes et de colonnes.
Ici, quelle est la différence entre un tableau et une matrice ?
Matrice implique généralement deux dimensions, tableaux sont généralement unidimensionnels, sauf indication contraire. UNE matrice est également un concept utilisé pour les mathématiques 3D hiérarchiques. UNE matrice a la taille m*n (2d). Un déployer a la taille m (1d), c'est donc un cas particulier.
A quoi servent les matrices ?
Matrices sont un moyen utile de représenter, manipuler et étudier des cartes linéaires entre des espaces vectoriels de dimension finie (si vous avez choisi une base). Matrices peut aussi représenter des formes quadratiques (c'est utile, par exemple, en analyse pour étudier la toile de jute matrices , qui nous aident à étudier le comportement des points critiques).
Conseillé:
Où sont enregistrés les tableaux de bord Kibana ?
Oui, les tableaux de bord Kibana sont enregistrés dans Elasticsearch sous l'index kibana-int (par défaut, vous pouvez remplacer cela dans le fichier config. js). Si vous souhaitez déplacer vos tableaux de bord Kibana vers un autre cluster ES, vous avez deux options : Exporter manuellement les tableaux de bord
Que sont les tableaux et les graphiques dans Excel ?
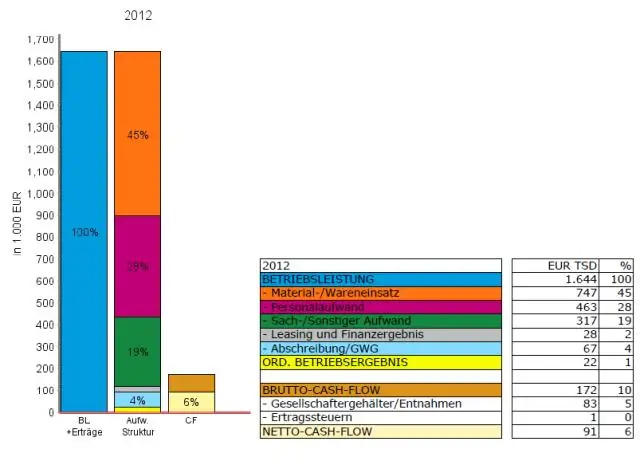
Les diagrammes et les graphiques sont des représentations visuelles des données de la feuille de calcul. Ces graphiques vous aident à comprendre les données d'une feuille de calcul en affichant des modèles et des tendances difficiles à voir dans les données. Les graphiques sont utilisés pour illustrer les tendances au fil du temps, et les graphiques illustrent des modèles ou contiennent des informations sur la fréquence
Quelles sont les règles de base pour nommer les tableaux ?

Les règles de base pour nommer les tableaux sont les suivantes : Le type de données peut être n'importe quel type de données valide tel que int, float, char structure ou union. Le nom d'un tableau doit suivre les règles de nommage des variables. la taille du tableau doit être zéro ou un entier positif constant
Quelles sont les notes du conférencier, écrivez son objectif et quels sont les éléments clés à retenir sur les notes du conférencier ?

Les notes du conférencier sont un texte guidé que le présentateur utilise lors de la présentation d'une présentation. Ils aident le présentateur à se rappeler des points importants tout en faisant une présentation. Ils apparaissent sur la diapositive et ne peuvent être consultés que par le présentateur et non par le public
Où sont stockés les tableaux de bord Kibana ?

Oui, les tableaux de bord Kibana sont enregistrés dans Elasticsearch sous l'index kibana-int (par défaut, vous pouvez remplacer cela dans le fichier config. js). Si vous souhaitez déplacer vos tableaux de bord Kibana vers un autre cluster ES, vous avez deux options : Exporter manuellement les tableaux de bord
