
- Auteur Lynn Donovan [email protected].
- Public 2023-12-15 23:46.
- Dernière modifié 2025-01-22 17:24.
UNE probabilite conditionnelle est le probabilité qu'un événement s'est produit, en tenant compte des informations supplémentaires sur le résultat de l'expérience. Deux événements A et B sont indépendant si la probabilité P(A∩B) de leur intersection A ∩ B est égal au produit P(A)·P(B) de leur individu probabilités.
En tenant compte de cela, la probabilité conditionnelle dépend-elle?
Probabilite conditionnelle est probabilité d'un deuxième événement étant donné qu'un premier événement s'est déjà produit. Cette est la probabilité conditionnelle avec deux dépendant événements. UNE dépendant événement est lorsqu'un événement influence le résultat d'un autre événement dans un probabilité scénario.
Sachez également, quelle est la formule pour la probabilité conditionnelle d'événements qui ne sont pas indépendants ? Dans le cas où événements A et B sont indépendant (où un événement A a non effet sur le probabilité d'événement B), le probabilité conditionnelle d'événement B donné un événement A est simplement le probabilité d'événement B, c'est-à-dire P(B). P(A et B) = P(A)P(B|A).
Par là, que signifie conditionnellement indépendant ?
En d'autres termes, et sont conditionnellement indépendant donnée si et seulement si, étant donné la connaissance qui se produit, la connaissance de la survenue ne fournit aucune information sur la probabilité de survenance, et la connaissance de la survenue ne fournit aucune information sur la probabilité de la survenance. se produisant.
L'indépendance implique-t-elle une indépendance conditionnelle ?
3 réponses. L'indépendance fait ne pas implique une indépendance conditionnelle : par exemple, indépendant les variables aléatoires sont rarement indépendant sous condition sur leur somme ou sur leur maximum.
Conseillé:
Que sont les contrôles Quels sont les différents types de contrôles en avance Java ?

Différents types de contrôles dans AWT Button. Toile. Case à cocher. Choix. Récipient. Étiqueter. Lister. Barre de défilement
Comment expliquez-vous les probabilités aux élèves ?
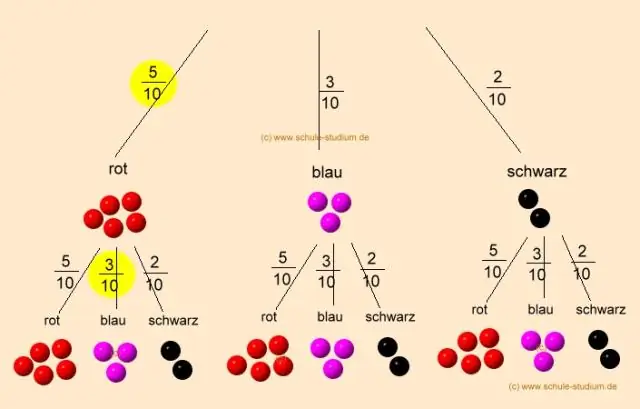
La probabilité est généralement exprimée sous la forme d'un rapport entre le nombre de résultats probables et le nombre total de résultats possibles. Demandez aux élèves s'ils peuvent donner un exemple de probabilité. Pour aider les élèves à comprendre les probabilités, travaillez sur le problème suivant en classe : Imaginez que vous êtes monté à bord d'un avion
Quelles sont les notes du conférencier, écrivez son objectif et quels sont les éléments clés à retenir sur les notes du conférencier ?

Les notes du conférencier sont un texte guidé que le présentateur utilise lors de la présentation d'une présentation. Ils aident le présentateur à se rappeler des points importants tout en faisant une présentation. Ils apparaissent sur la diapositive et ne peuvent être consultés que par le présentateur et non par le public
Quels sont les défis auxquels les managers sont confrontés lorsqu'ils communiquent avec des équipes virtuelles ?

Vous trouverez ci-dessous un aperçu des défis de l'équipe virtuelle et de leur gestion. Réunions en ligne faciles et gratuites. Gratuit jusqu'à 100 participants. Mauvaise communication. Manque d'interaction sociale. Manque de confiance. Des équipes multiculturelles diversifiées. Perte de moral et d'esprit d'équipe. Distance physique. Différences de fuseau horaire
Pourquoi enseigne-t-on les probabilités ?

L'apprentissage des probabilités dans les premières années fournira aux élèves une base plus solide pour une étude plus approfondie des statistiques et des probabilités au lycée. Le défi consiste à établir des relations avec les enfants et à les engager dans des expériences d'apprentissage dans lesquelles ils construisent leur propre compréhension des concepts de probabilité
