Vidéo: Comment prouver que les diagonales d'un losange se coupent en leur milieu ?
2024 Auteur: Lynn Donovan | [email protected]. Dernière modifié: 2023-12-15 23:46
Dans un losange tout les côtés sont égaux et les côtés opposés sont parallèles. Plus loin un rhombe est aussi un parallélogramme et présente donc les propriétés d'un parallélogramme et cela les diagonales d'un parallélogramme se coupent en leur milieu.
En conséquence, les diagonales d'un losange se coupent-elles en leur milieu ?
Dans tous rhombe , les diagonales (lignes reliant les coins opposés) se couper en deux à angle droit (90°). C'est-à-dire, chaque diagonale coupe le autre en deux parties égales, et l'angle où ils se croisent est toujours de 90 degrés. Dans la figure ci-dessus, faites glisser n'importe quel sommet pour remodeler le rhombe et convainquez-vous qu'il en est ainsi.
Deuxièmement, les diagonales des losanges sont-elles perpendiculaires ? Propriétés d'un Rhombe Les diagonales sommes perpendiculaire à et se couper en deux. Les angles adjacents sont supplémentaires (par exemple, A + ∠B = 180°). UNE rhombe est un parallélogramme dont diagonales sommes perpendiculaire l'un à l'autre.
En tenant compte de cela, comment prouvez-vous que les diagonales d'un losange sont des bissectrices perpendiculaires ?
Preuve que le les diagonales d'un losange sont perpendiculaires Suite de ci-dessus preuve : Les parties correspondantes des triangles congrus sont congrues, donc les 4 angles (ceux du milieu) sont congrus. Cela conduit au fait qu'ils sont tous égaux à 90 degrés, et le diagonales sommes perpendiculaire l'un à l'autre.
Le losange est-il un parallélogramme ?
DÉFINITION: UN rhombe est un parallélogramme avec quatre côtés congrus. THÉORÈME: Si un parallélogramme est un rhombe , chaque diagonale coupe en son milieu une paire d'angles opposés. THÉORÈME Converse: Si un parallélogramme a des diagonales qui coupent en leur milieu une paire d'angles opposés, c'est un rhombe.
Conseillé:
Les diagonales se coupent-elles toujours en leur milieu dans un parallélogramme ?
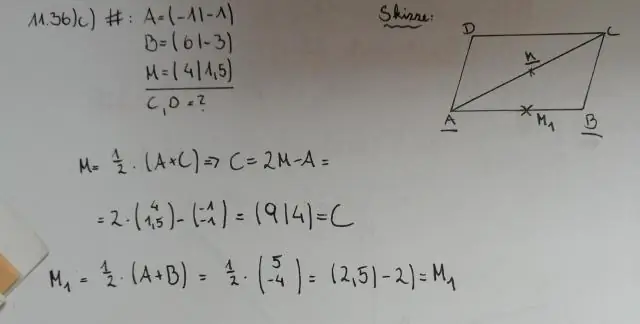
Dans tout parallélogramme, les diagonales (lignes reliant les coins opposés) se coupent en leur milieu. C'est-à-dire que chaque diagonale coupe l'autre en deux parties égales. Dans la figure ci-dessus, faites glisser n'importe quel sommet pour remodeler le parallélogramme et vous convaincre que c'est le cas
Les diagonales du parallélogramme se coupent-elles en leur milieu à 90 ?
Dans tout losange, les diagonales (lignes reliant les coins opposés) se coupent à angle droit (90°). C'est-à-dire que chaque diagonale coupe l'autre en deux parties égales, et l'angle où elles se croisent est toujours de 90 degrés
Quels parallélogrammes ont des diagonales qui se coupent en leur milieu ?
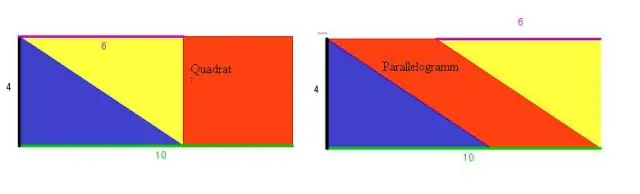
Si deux côtés adjacents d'un parallélogramme sont égaux, alors c'est un losange. Ce test est souvent considéré comme la définition d'un losange. Un quadrilatère dont les diagonales se coupent à angle droit est un losange
Comment prouver un code linéaire ?
Un code linéaire est généralement défini comme un sous-espace de Fn pour un champ F (puisque vous parlez de bits, vous pouvez prendre F=F2={0,1}). Le code C généré par une matrice génératrice G est l'étendue des lignes de G. L'étendue d'un ensemble de vecteurs dans Fn est un sous-espace de Fn, donc C est un code linéaire
Comment prouver une induction forte ?
Le principe d'induction forte dit que vous pouvez prouver un énoncé de la forme : P(n) pour chaque entier positif n. comme suit : Cas de base : P(1) est vrai. Pas inductif fort : Supposons que k soit un entier positif tel que P(1),P(2),,P(k) soient tous vrais. Montrer que P(k+1) est vrai